CSC2626 Imitation Learning for Robotics
Week 12: Representation Learning for Imitation & Provable Generalization
Today’s Agenda
Representation Learning for Imitation
- Is it better to separate representation learning from policy learning?
Provable generalization
- PAC-Bayes generalization bounds
Robustness and safety
- Robustness as stability
Learning dense representations for manipulation
Dense Object Nets: Learning Dense Visual Object Descriptors By and For Robotic Manipulation. Florence, Manuelli, Tedrake. 2018
Learning policies on top of pretrained representations
Self-Supervised Correspondence in Visuomotor Policy Learning. Florence, Manuelli, Tedrake. 2020
Another example of policy learning on pretrained representations
Can we show theoretically that representation learning helps?
[switch to notes]
Today’s Agenda
Representation Learning for Imitation
- Is it better to separate representation learning from policy learning?
Provable generalization
- PAC-Bayes generalization bounds
Robustness and safety
- Robustness as stability
PAC-Bayes generalization bounds

PAC-Bayes Control: Learning Policies that Provably Generalize to New Environments. Majumdar et al. 2020
PAC-Bayes Bound Applied to Control

PAC-Bayes Control: Learning Policies that Provably Generalize to New Environments. Majumdar et al. 2020
PAC-Bayes Example
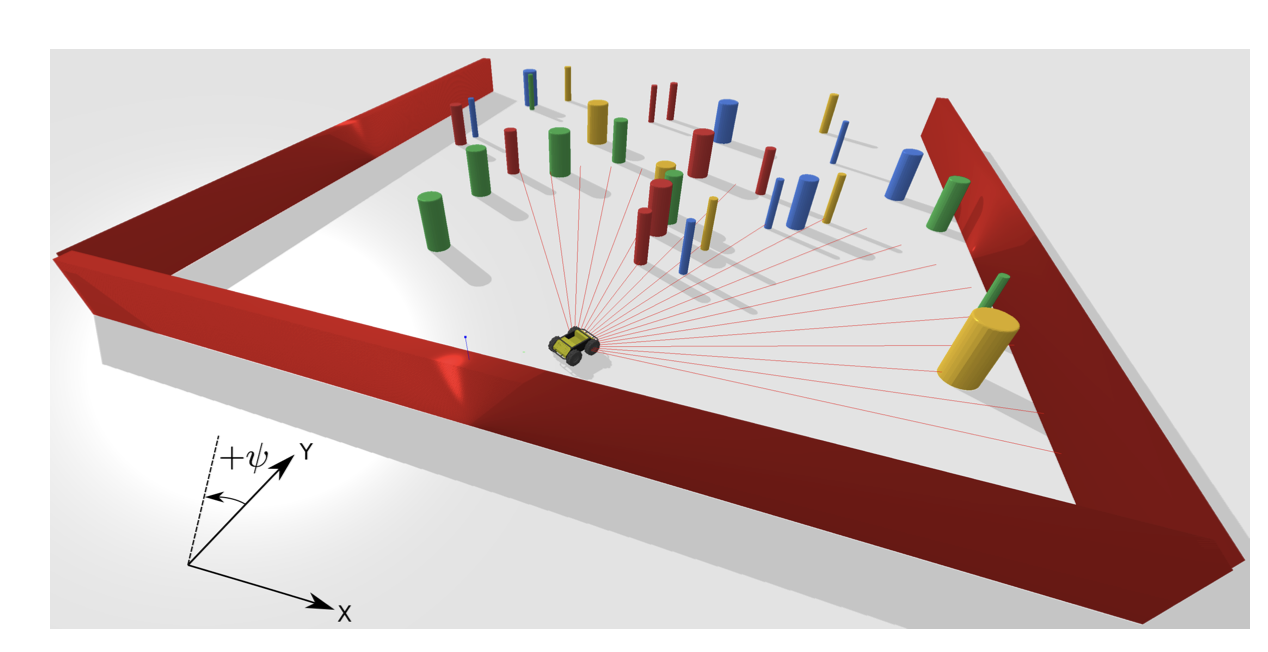
PAC-Bayes Control: Learning Policies that Provably Generalize to New Environments. Majumdar et al. 2020
PAC-Bayes Control for Visuomotor Policies
Generalization Guarantees for Imitation Learning. Ren, Veer, Majumdar. CoRL 2020.
Today’s Agenda
Representation Learning for Imitation
- Is it better to separate representation learning from policy learning?
Provable generalization
- PAC-Bayes generalization bounds
Robustness and safety
- Robustness as stability
What does it mean for a policy to be robust?
• The system (policy, dynamics) must be such that the policy will achieve its goal point, even if a family of disturbances/noise affect it
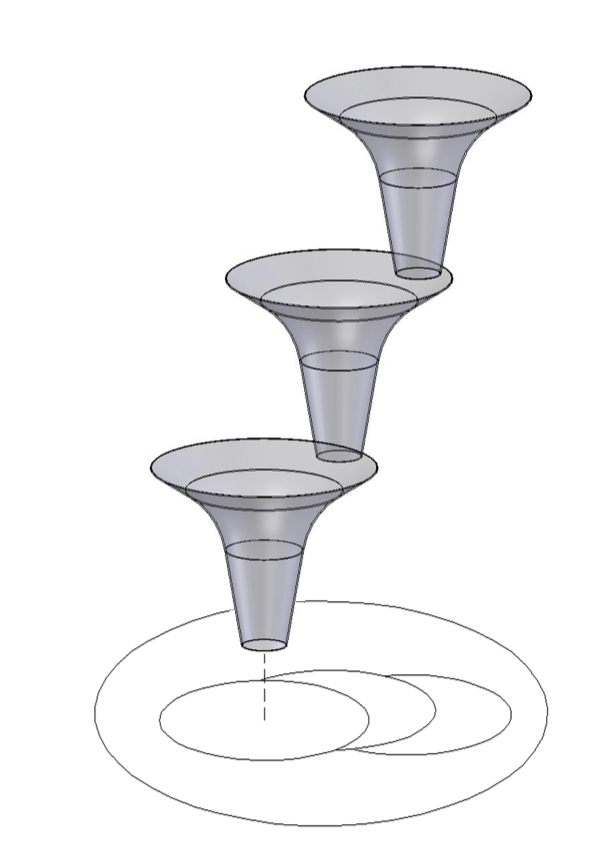
Composition of robust policies
LQR Trees. Tedrake, RSS 2005.
Robustness as stability of dynamical systems
- Global asymptotic stability to a goal: the region of attraction includes all states. The system will converge to the goal, no matter where it starts from.
- How to ensure global asymptotic stability:
- Show that there exists a positive energy (Lyapunov) function that
- Decreases over time along the system trajectories
- And will become 0 at the convergence point
Examples of Lyapunov functions
[switches to notes]
Two examples of learning Lyapunov functions

