Main Hypothesis
Shared autonomy can improve human performance without any assumptions about:
dynamics,
the human’s policy,
the nature of the goal.
Week 10: Shared Autonomy and Human-in-the-Loop Learning
• Shared autonomy for assistive robotics
• Shared autonomy with human in the loop in deep RL
• Hindsight optimization and interactive goal prediction
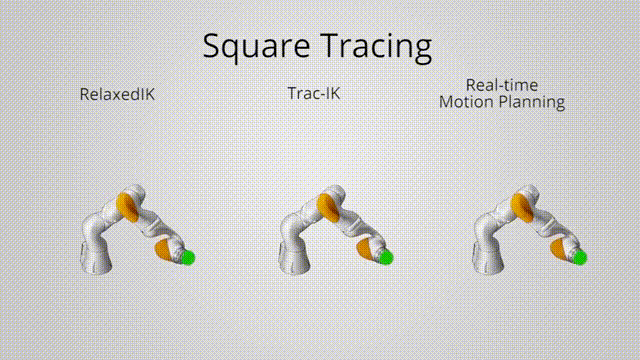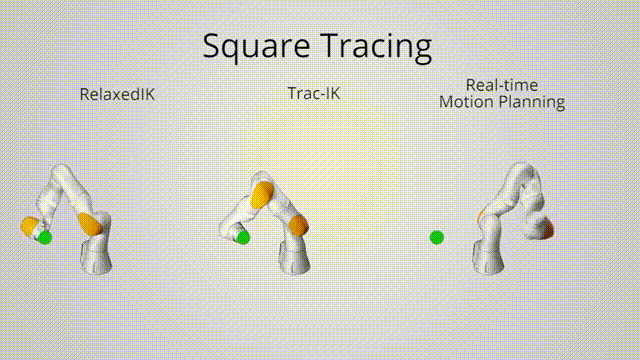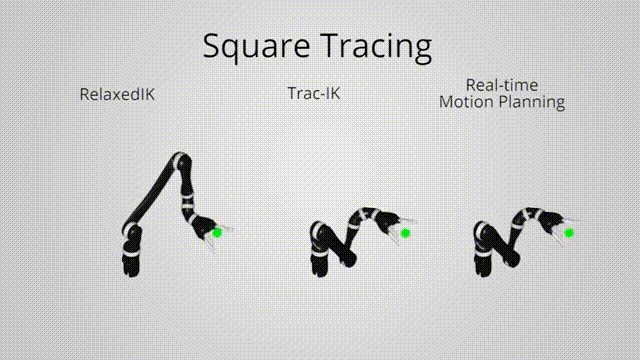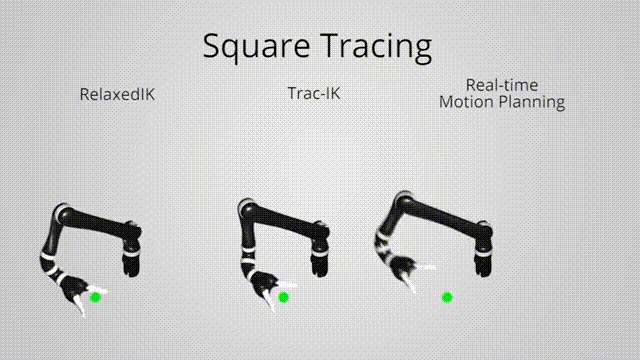
• Relaxed inverse kinematics for fluid interaction with robot arms
Siddharth Reddy, Anca Dragan, Sergey Levine UC Berkeley
Presented by Ioan Andrei Bârsan on February 22, 2019
iab@cs.toronto.edu
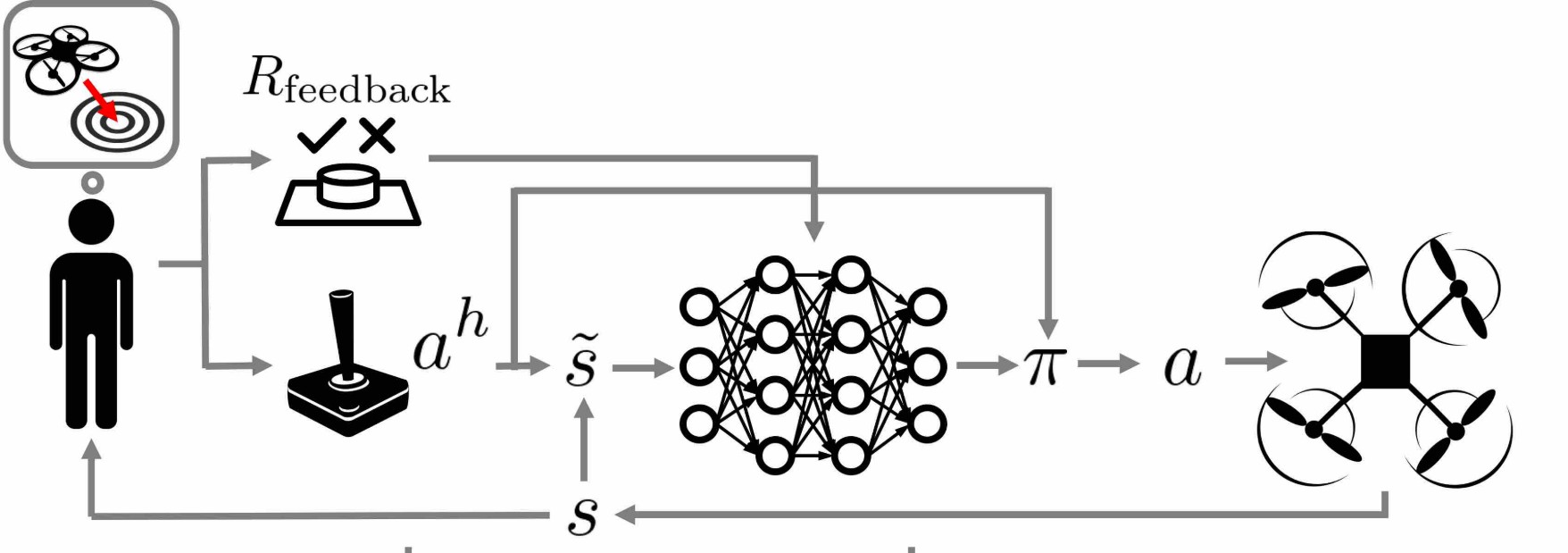

How can a robot collaborating with a human infer the human’s goals with as few assumptions as possible?
• Hard: Actuating a robot with many DoF and/or unfamiliar dynamics.
• Hard: Specifying a goal formally (e.g., coordinates).
• Easy: Demonstrating the goal indirectly.
• …let the machine figure out what I want!

Image source: “Multihierarchical Interactive Task Planning. Application to Mobile Robotics” Galindo et al., 2008

https://www.foddy.net/Athletics.html or Google “qwop”
• Recall: Want to demonstrate the goal indirectly with minimal assumptions.
• → We expect the computer to start helping while it is still learning.
• Challenge #1: How to actually infer user’s goal?
• Challenge #2: How can we learn this online with low latency?
Shared autonomy can improve human performance without any assumptions about:
dynamics,
the human’s policy,
the nature of the goal.
\[ R(s, a, s') = \underbrace{R_{\text{general}}(s, a, s')}_{\text{known}} + \underbrace{R_{\text{feedback}}(s, a, s')}_{\text{unknown, but observed}} \]
\(\qquad \qquad \quad \uparrow\)
Agent’s reward
(what we want to maximize)
\(\qquad \qquad \qquad \uparrow\)
Handcrafted “common sense”
knowledge: do not crash, do
not tip, etc.
\(\uparrow\)
Stuff inferred from the human
(Main focus of this paper!)
\[ \underbrace{R_{\text{feedback}}(s, a, s')}_{\text{unknown, but observed}} \]
Needs
virtual
“user”!
• The authors introduce three variants of their method:
Known goal space, known user policy.
Known goal space, unknown user policy.
Unknown goal space, unknown user policy.
Based on Q-Learning.
User input has two roles:
A prior policy we should fine-tune.
A sensor which can be used to decode the goal.
Short version: Like Q-Learning, but execute closest high-value action to the user’s input, instead of highest-value action.
Known goal space & user policy → exact goal.
Known goal space & unknown policy → predicted goal (pretrained LSTM).
Unknown goal space & policy → the user’s input (main focus)
Virtual experiments with Lunar Lander in OpenAI gym.
Physical experiments with an actual drone.
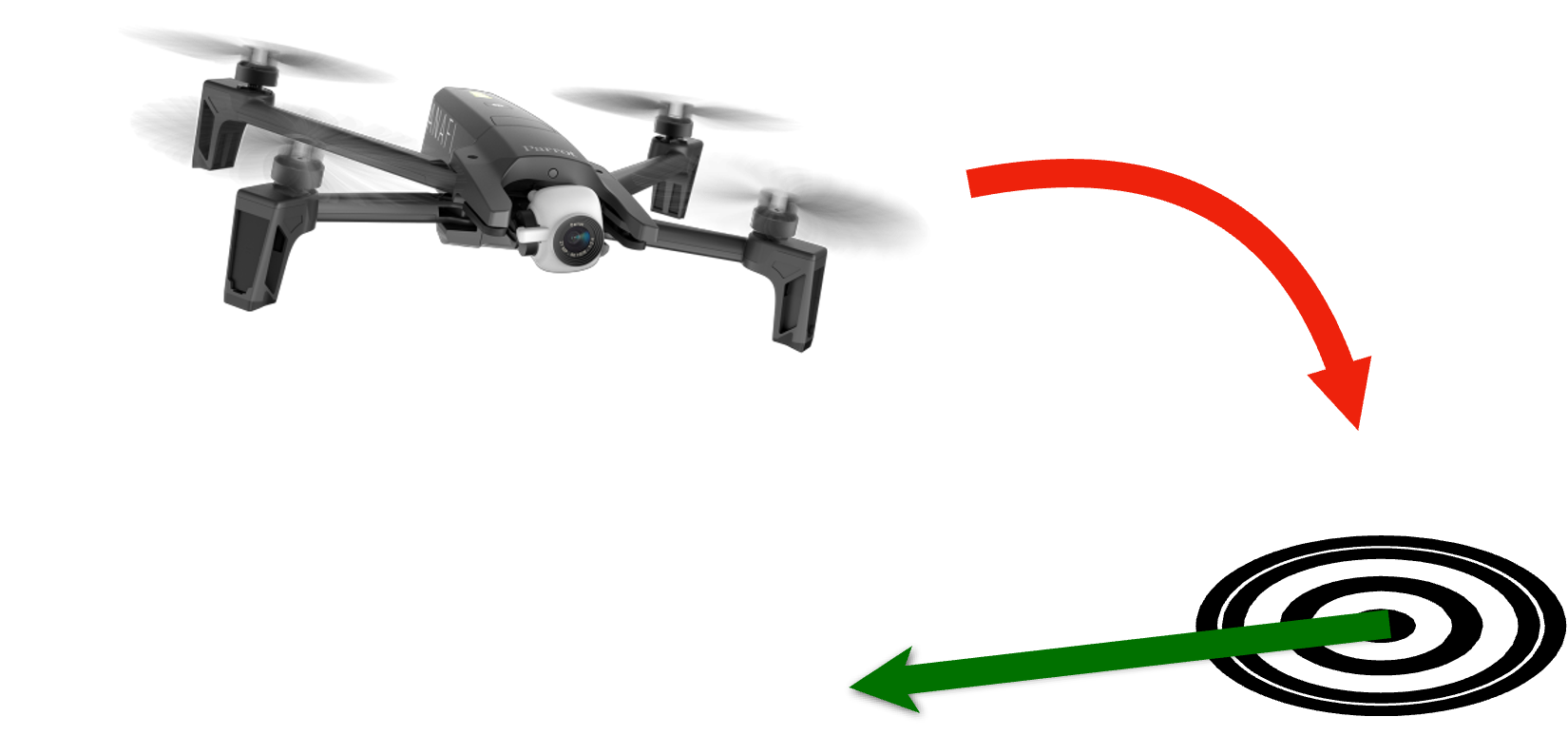
Goal: Land drone on pad facing a certain way.
Pilot: Human, knows target orientation.
Copilot: Our Agent, knows where pad is, but not target orientation.
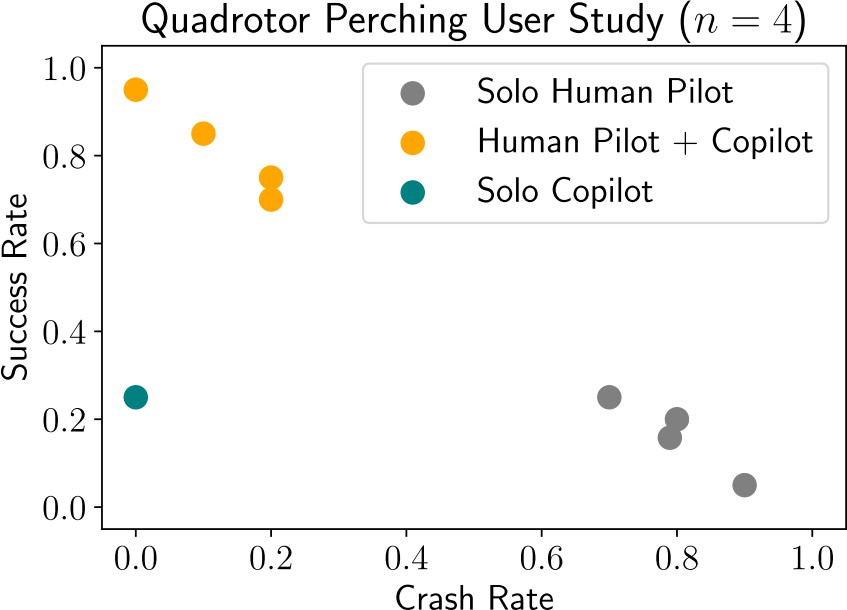
Important observation: Only n = 4 humans in drone study.
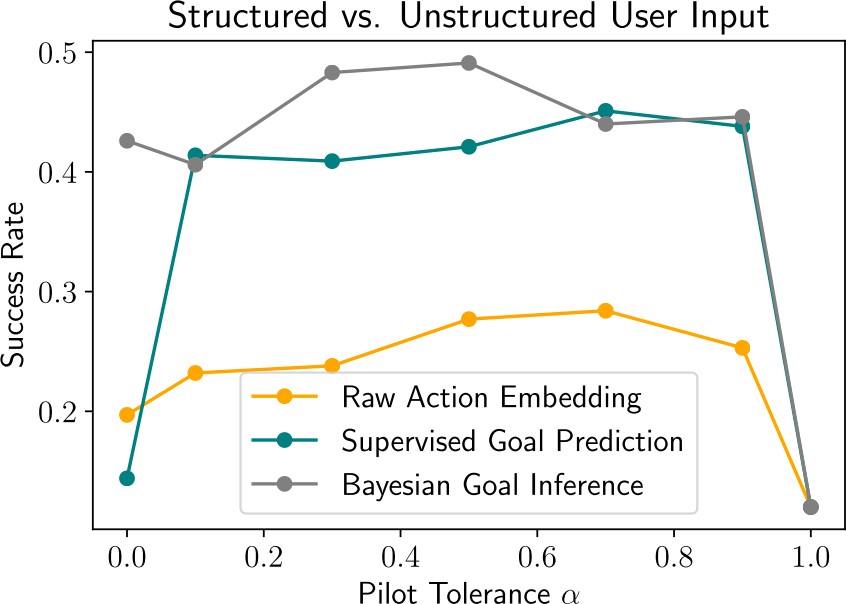
Higher alpha means we take any action. α = 1.0 means we ignore the pilot.
Experimented in virtual environment.
Good results even when making no assumptions about user/goal.
Writing is very clear!
Possible applications in many fields, including e.g. prosthetics, wheelchairs.
Source code released on GitHub!
User studies could have had more participants.
Could have shown results on more Gym environments.
Solution does not generalize to sophisticated long-term goals.
Q&A, if time permits it.
Project website: https://sites.google.com/view/deep-assist
Video of computer-assisted human piloting the lander.





Noisy, insufficient degrees of freedom, tedious
Image credit: Javdani RSS2015 talk
 User Input
User Input
+
 Autonomous Assistance
Autonomous Assistance
=
 Achieve Goal
Achieve Goal
 User Input
User Input
+
 Autonomous Assistance
Autonomous Assistance
=
 Achieve Goal
Achieve Goal
Predict goal Assist for single goal
[Dragan and Srinivasa 13]
[Kofman et al. 05]
[Kragic et al. 05]
[Yu et al. 05]
[McMullen et al. 14]
…
+
 Autonomous Assistance
Autonomous Assistance
=
 Achieve Goal
Achieve Goal
Predict goal Assist for single goal
[Dragan and Srinivasa 13]
[Kofman et al. 05]
[Kragic et al. 05]
[Yu et al. 05]
[McMullen et al. 14]
…
Predict goal distribution Assist for distribution
[Hauser 13]
This work!
+
 Autonomous Assistance
Autonomous Assistance
=
 Achieve Goal
Achieve Goal
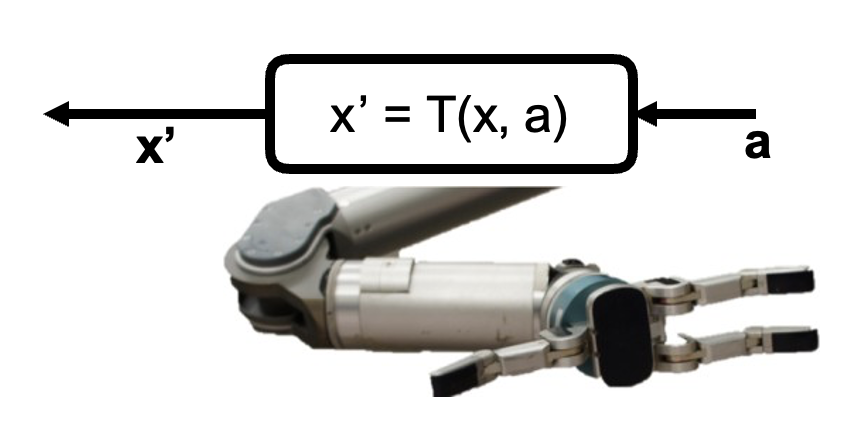
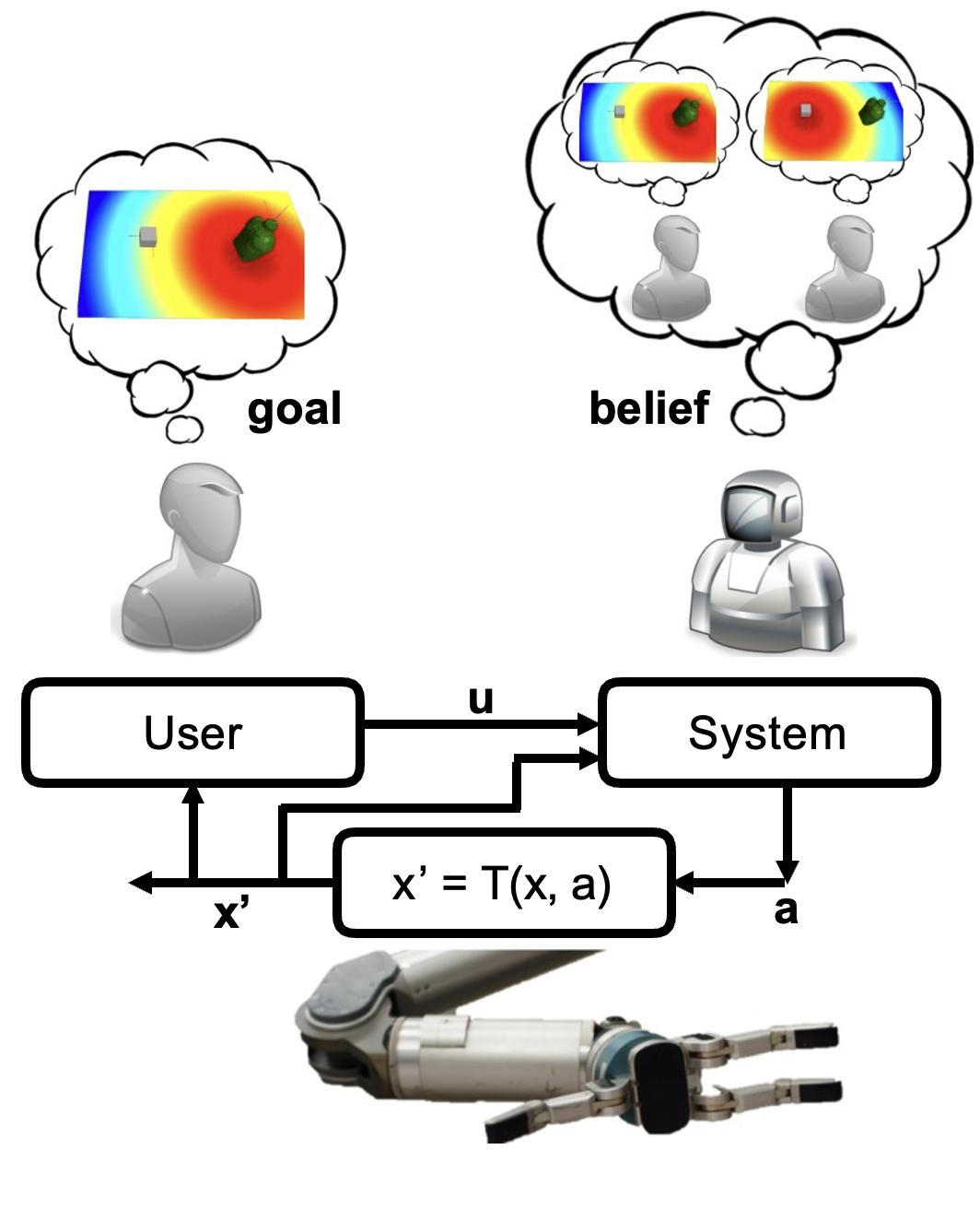
System dynamics: \(x' = T(x, a)\)
User (MDP) as \((X, U, T, C_g^{\text{usr}})\)
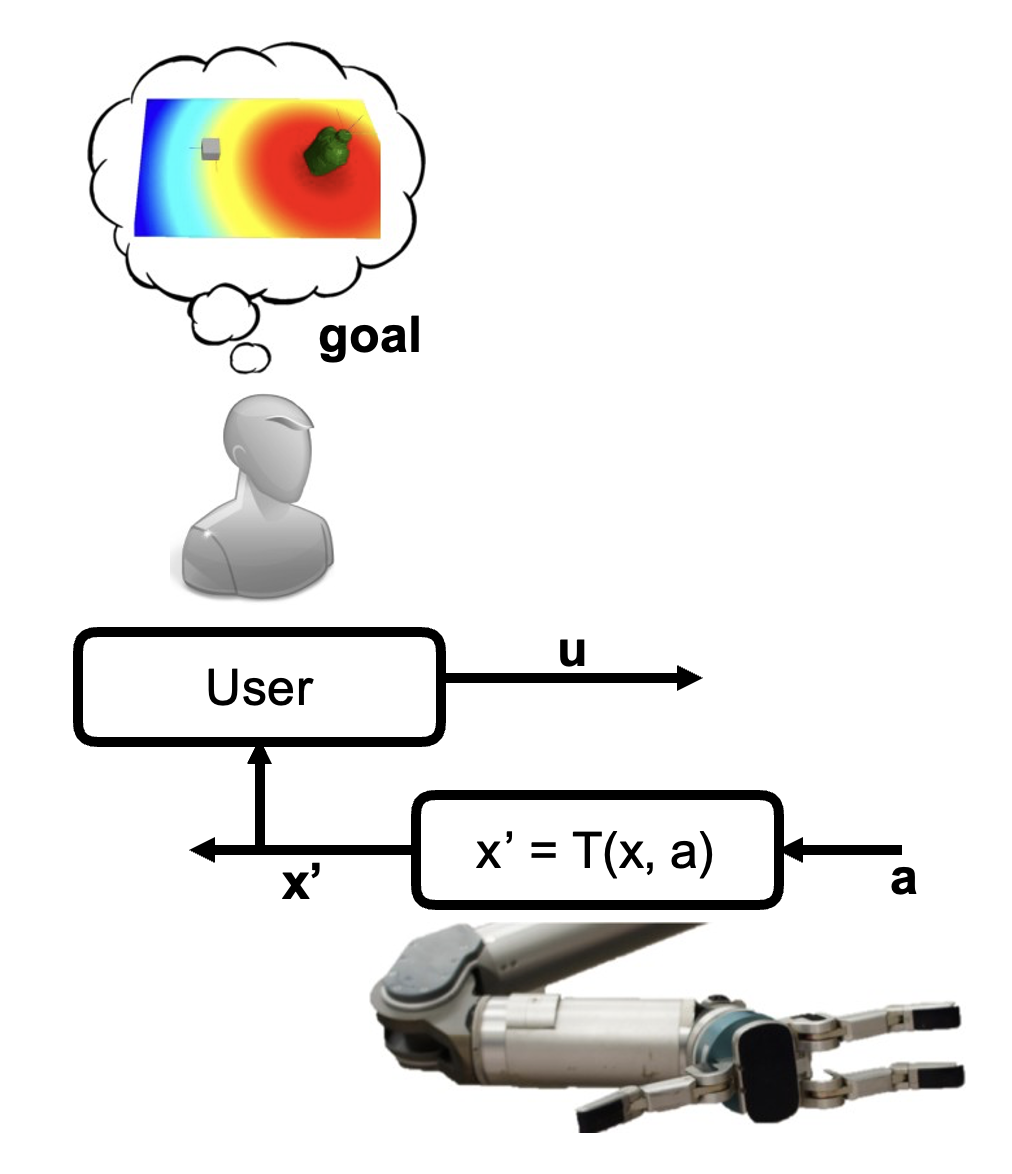
System dynamics: \(x' = T(x, a)\)
User (MDP) as \((X, U, T, C_g^{\text{usr}})\)
System (POMDP) as \((S, A, T, C^{\text{rob}}, U, \Omega)\)
\(p(g|\xi^{0 \to t}) = \frac{p(\xi^{0 \to t}|g)p(g)}{\sum_{g'} p(\xi^{0 \to t}|g')p(g')}\)
MDP solution:
\[V^{\pi^r}(s) = \mathbb{E}\left[\sum_t C^r(s_t, u_t, a_t) \mid s_0 = s\right]\]
\[V^*(s) = \min_{\pi^r} V^{\pi^r}(s)\]
POMDP solution:
\[V^{\pi^r}(b) = \mathbb{E}\left[\sum_t C^r(s_t, u_t, a_t) \mid b_0 = b\right]\]
\[V^*(b) = \min_{\pi^r} V^{\pi^r}(b)\]
HOP approximation:
\[V^{\text{HS}}(b) = \mathbb{E}_b\left[\min_{\pi^r} V^{\pi^r}(s)\right]\]
\[= \mathbb{E}_g[V_g(x)]\]
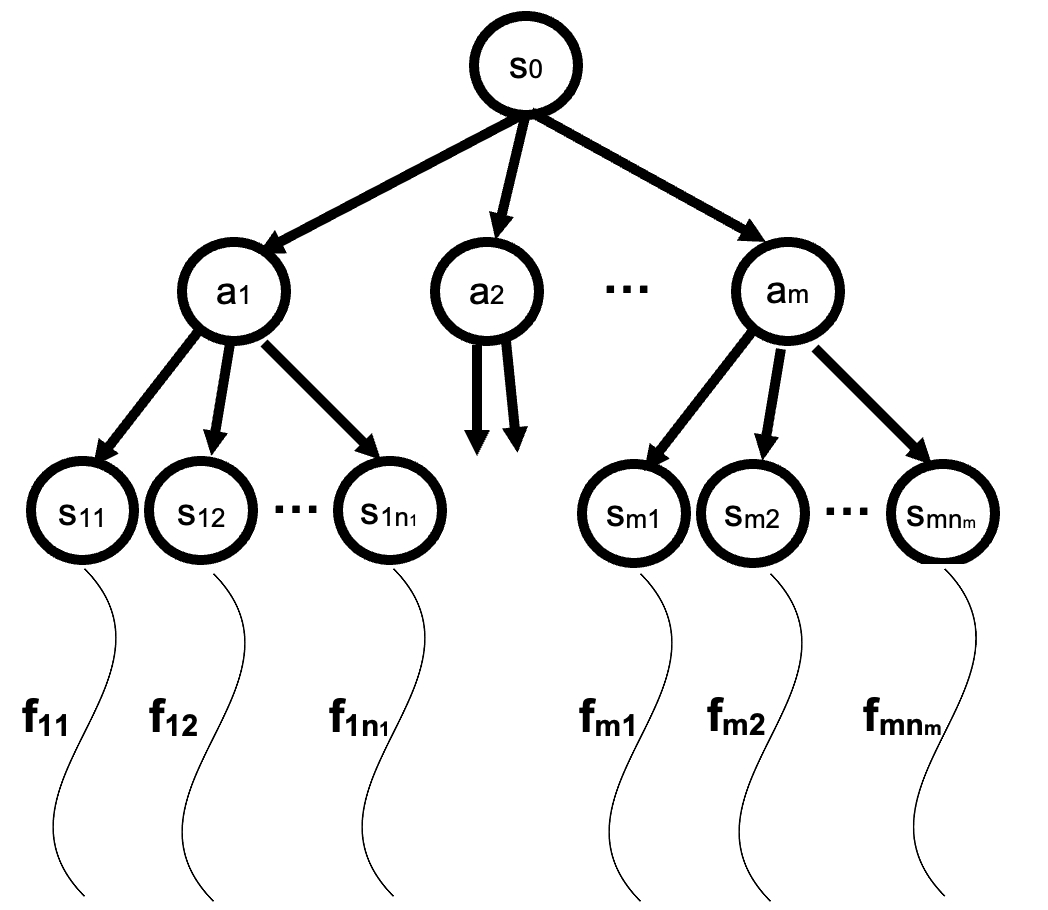
Deterministic
problem for
each future
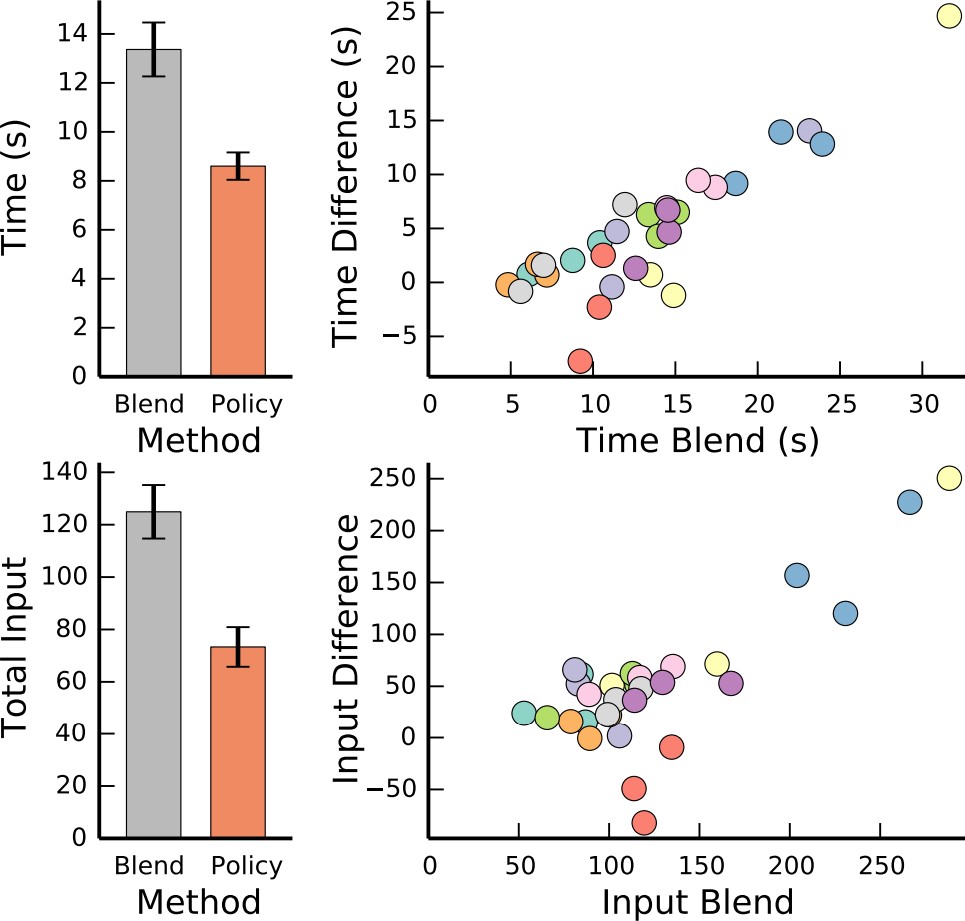
Compare with method that predicts one goal, the proposed method has:
Faster execution time
Fewer user inputs
Requires prior knowledge about the world:
a dynamics model that predicts the consequences of taking a given action in a given state of the environment;
the set of possible goals for the user;
the user’s control policy given their goal.
Suitable in constrained domains where where this knowledge can be directly hard-coded or learned.
Unsuitable for unstructured environments with ill-defined goals and unpredictable user behavior.
Javdani, S., Srinivasa, S. S., & Bagnell, J. A. (2015). Shared autonomy via hindsight optimization. Robotics science and systems: online proceedings, 2015.
RSS2015 talk: “Shared autonomy via hindsight optimization”
Javdani, S., Admoni, H., Pellegrinelli, S., Srinivasa, S. S., & Bagnell, J. A. (2018). Shared autonomy via hindsight optimization for teleoperation and teaming. The International Journal of Robotics Research, 37(7), 717-742.
ICAPS 2015 talk: “Hindsight Optimization for Probabilistic Planning with Factored Actions”
Forward Kinematics
A common robotic skeleton is a tree of rigid bones
The relative Euler angles of all the joints determine the end-effector
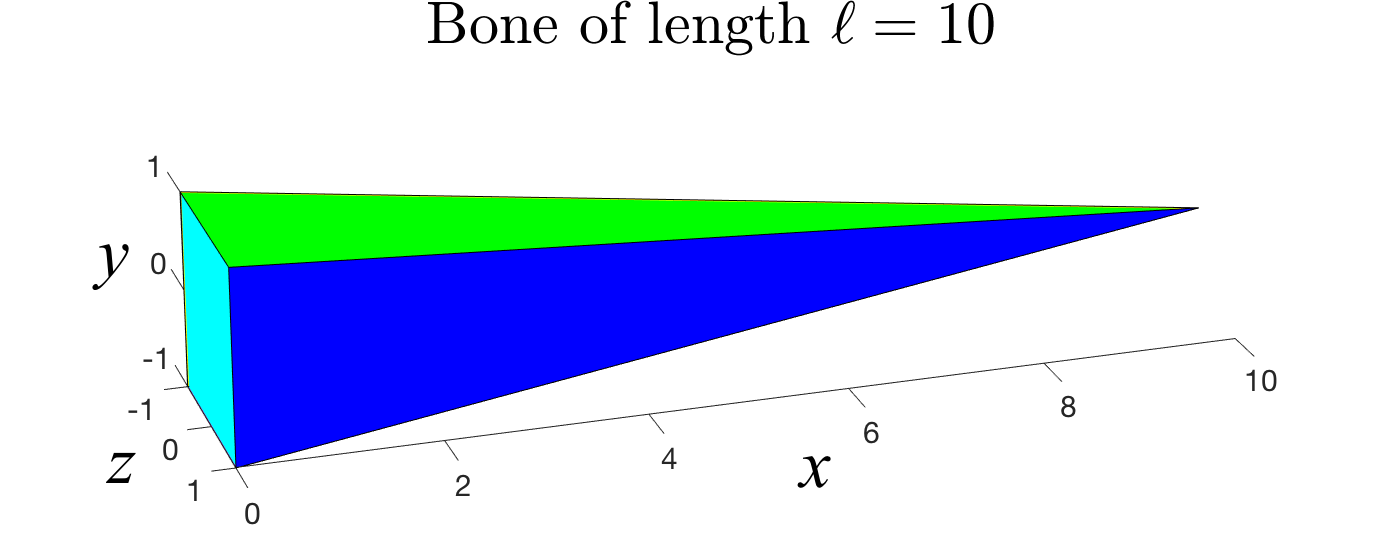
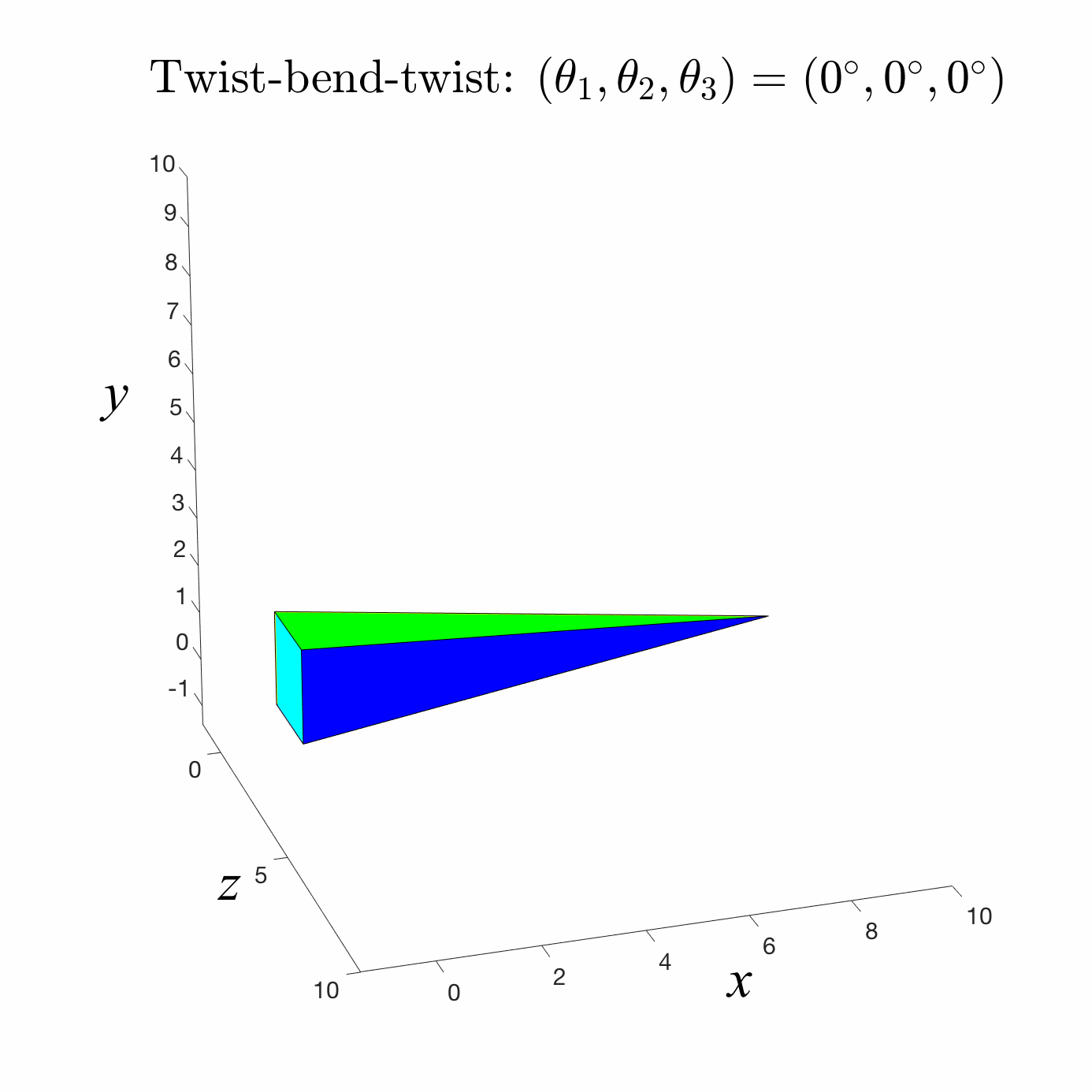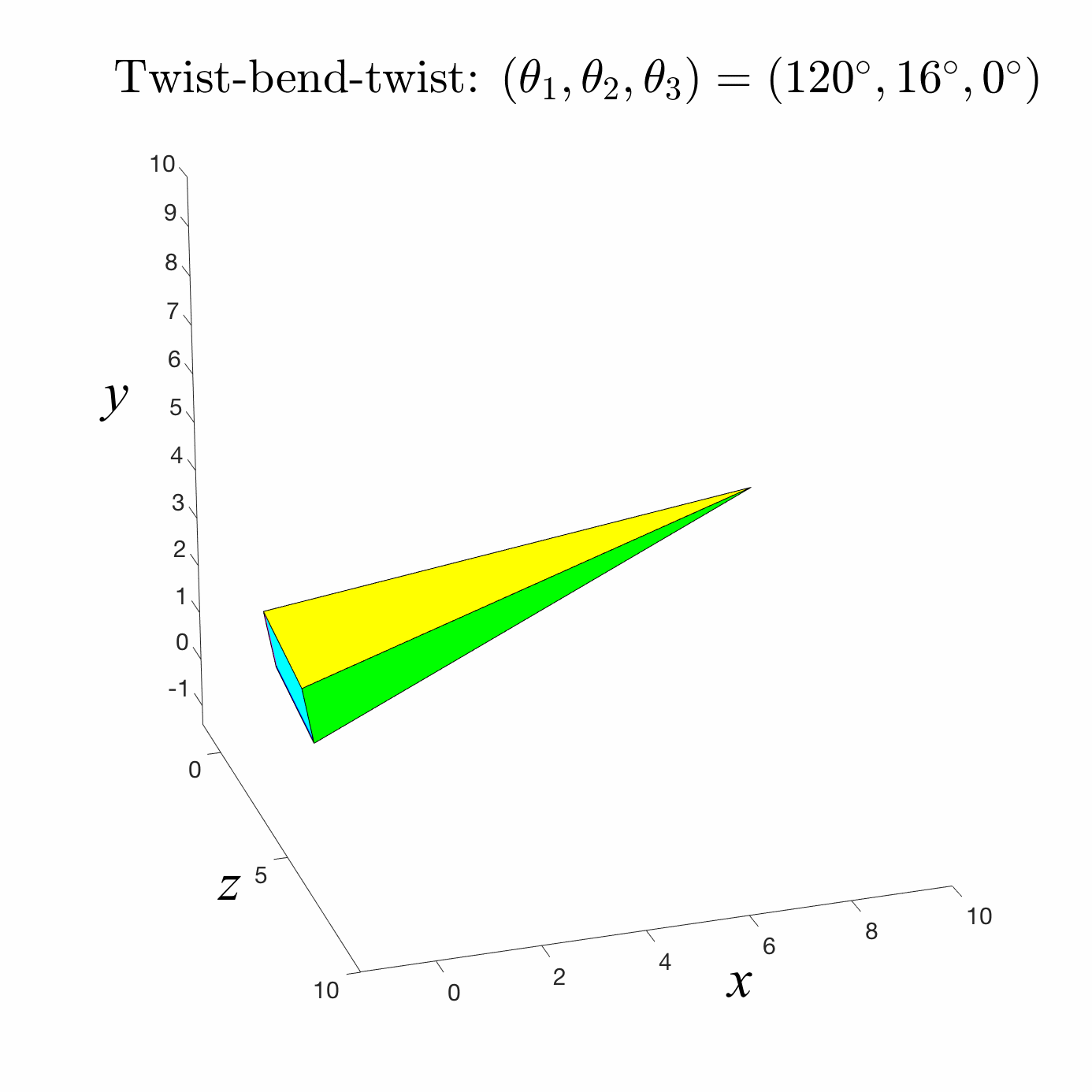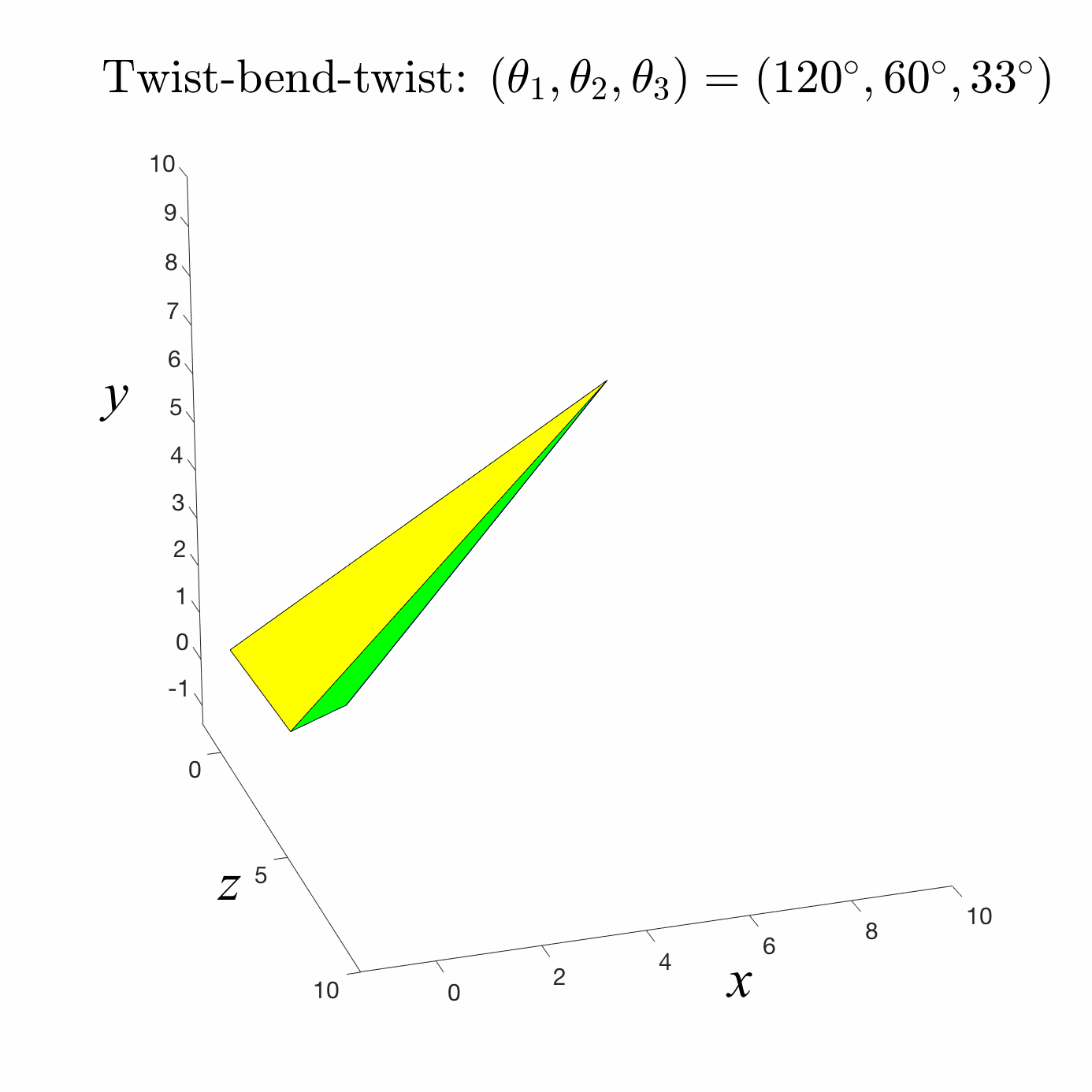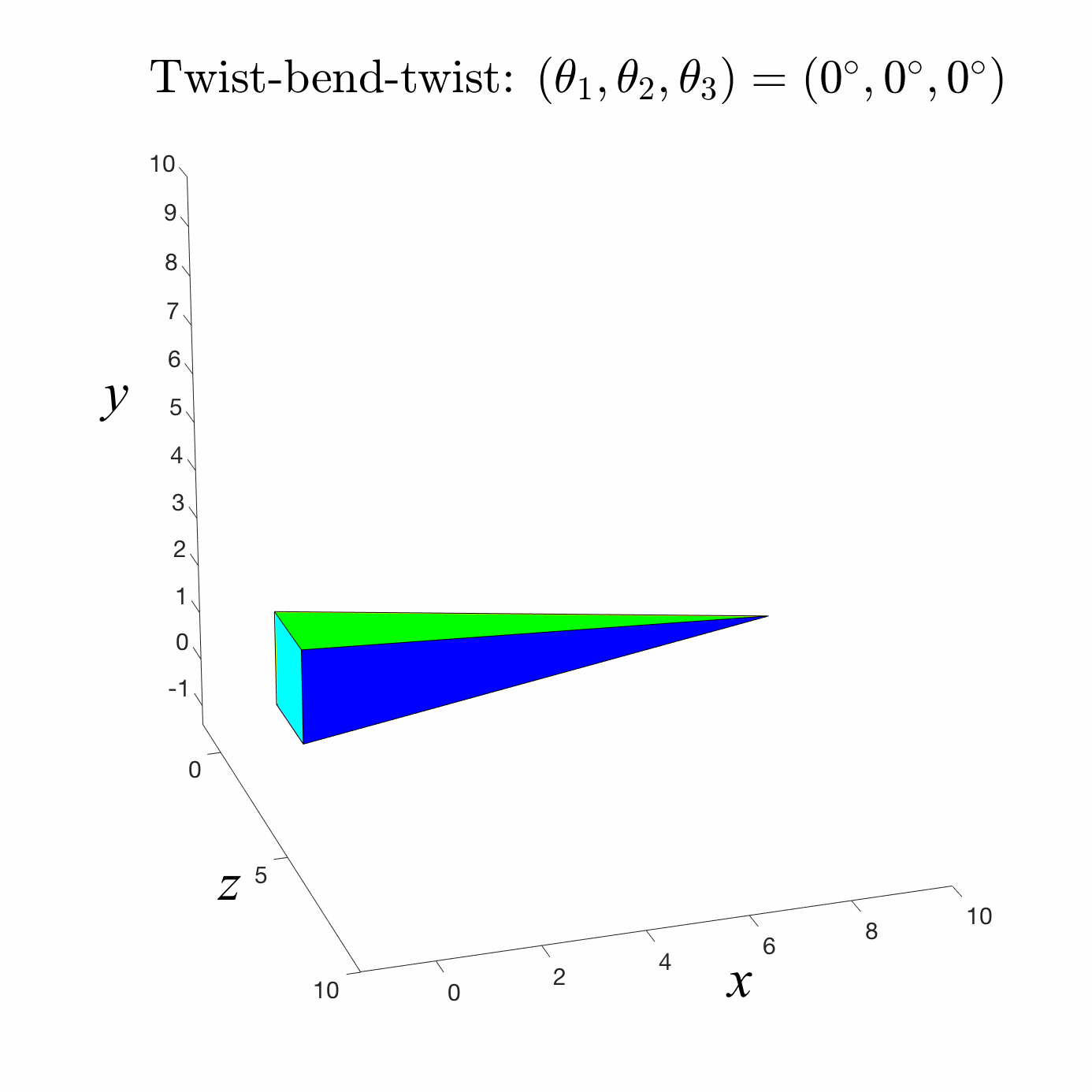
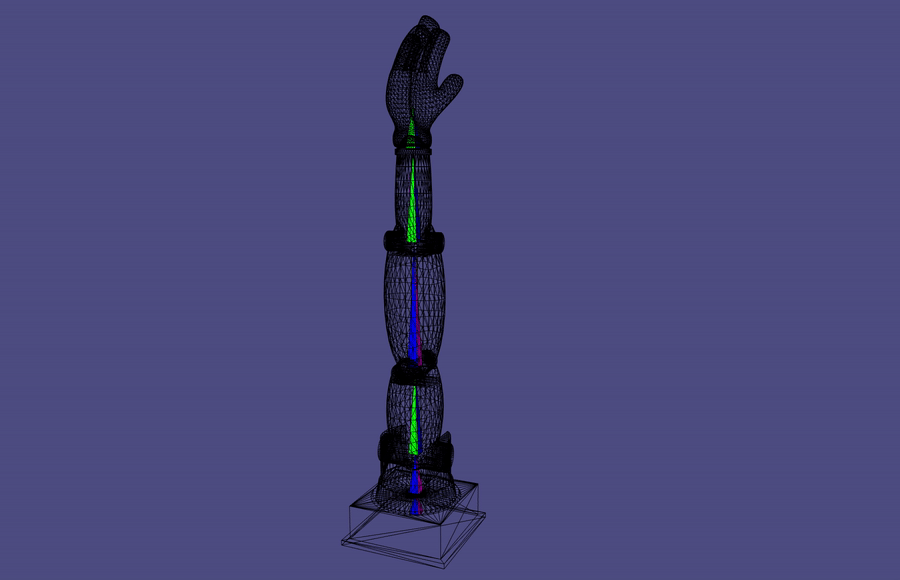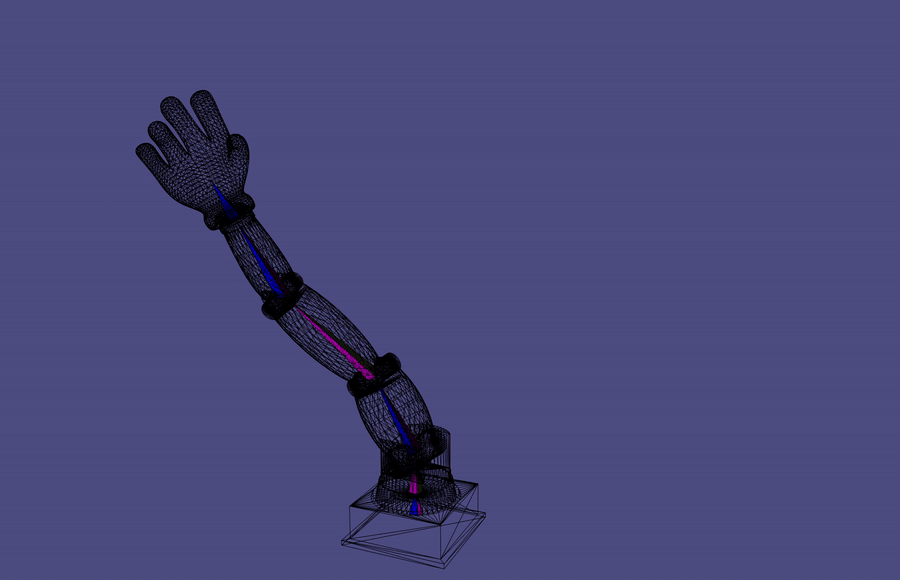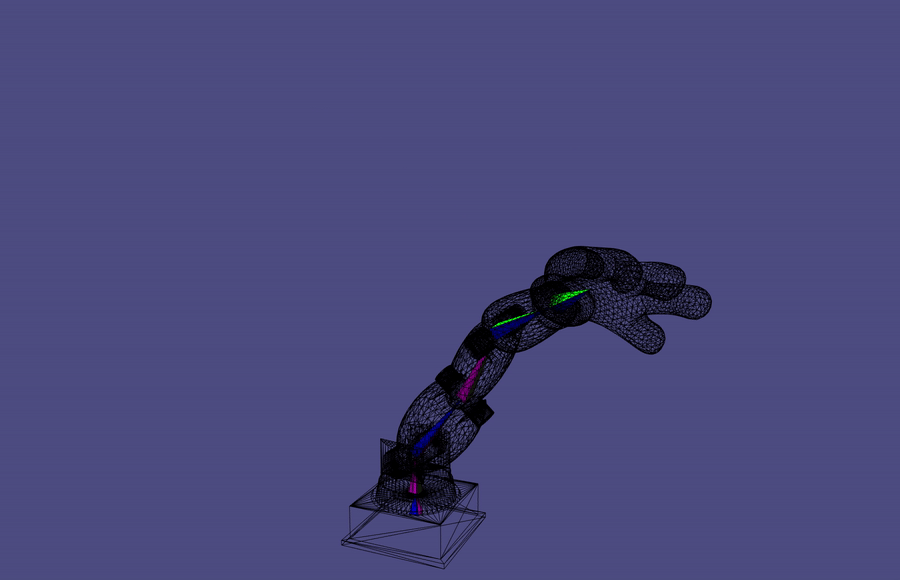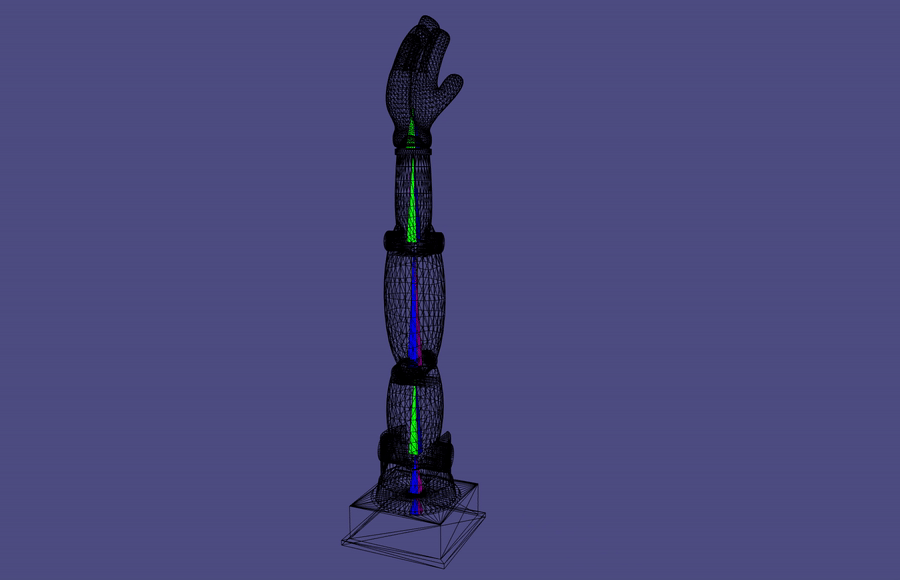
materials from https://github.com/alecjacobson/computer-graphics-csc418
Inverse Kinematics
We formulate the inverse kinematics function as: \(\Theta = IK(p)\) , which can be easily written in an analytic form for a simple tree skeleton.
Pose contains velocity?
Hard to find feasible state space?
In reality, IK is often treated as an optimization problem \[ \chi_p(\Theta) = \| p_g - FK(\Theta) \|_2 \]

Imitation learning using IK
Basic idea: Using IK to bridge between target pose and agent’s angles
Input: M (consecutive) expert (goal) poses
Output: M (consecutive) frames of agent’s euler joints
Constraints:
IK constraints (goal constraints)
Between-frames constraints
Imitation learning using IK
Direct point-to-point approach
TRAC-IK (previous state-of-the-art)
Pose2pose / frame2frame imitation learning
Problems
Self-collision
Time constraints
Self-collision

Discontinuities

Goal mistracking

Unpredictable behaviors 
\[ f(\Theta) = \sum_{i=1}^{k} w_i f_i(\Theta, \Omega_i) \]
Loss functions
End-effector position & orientation matching
Minimize joint velocity, acceleration, jerk
Self-collision loss (fast)
Singularity loss
Self-collision loss
Common approach: very slow
Relaxed IK:
Approximate how imminent the robot is to a collision state
Using simulated data to train a network to predict the distances between links
\[ \text{col}(\Theta) = \sum_{i,j} b \cdot \exp\left( -\frac{\text{dis}(l_i, l_j)^2}{2c^2} \right) \]

Kinematic singularities are well studied in robotics
Relaxed IK:
Find a metric that can approximate distance to a singularity
Jacobian’s condition number is used as a proxy distance to singularity
Why?
\[ \dot{\mathbf{x}} = \mathbf{J}(\Theta) \dot{\Theta} \]
Penalize condition values less than mean - b * std
Estimate mean, std from simulated data
Pros